Addition and Subtraction of Rational Numbers – Easy and Step-by-Step Rules with Examples

Published: 17 Oct 2025

Learning the basics and step by step rules for Addition and Subtraction of Rational Numbers help you solve many real-life math problems. This includes working with fractions, decimals, and negative numbers. In this post, we’ll guide you with step-by-step solutions, clear examples with daily life problems, and fun practice questions to make everything easy and understandable!

“Scroll down to explore add and subtract rational numbers with easy rules and step by step explanation!”

Table of Content

How to Add and Subtract Rational Numbers
Full Example with All Steps Combined
Real-Life Examples
Practice Questions

How to Add and Subtract Rational Numbers

To add or subtract rational numbers, we follow a few simple steps. The operation works almost the same way as integer operations (see integer operations here), but with the extra step of considering denominators. Depending on whether the rational numbers have the same denominator, different denominators, or include negative or mixed numbers, the steps and methods are followed accordingly.

1. When denominators are the same:

To add or subtract rational numbers with the same denominator, follow these steps:

Keep the denominator the same.
Add or subtract the numerators.
Examples:

Addition	Subtraction
General Form $ \dfrac{a}{c} + \dfrac{b}{c} = \frac{a+b}{c} $	General Form $ \frac{a}{c} – \frac{b}{c} = \frac{a-b}{c} $
Example: $ \begin{aligned} \dfrac{3}{7} + \dfrac{2}{7} & = \dfrac{3+2}{7} \\ & = \dfrac{5}{7} \end{aligned} $	Example: $ \begin{aligned} \dfrac{3}{7} – \dfrac{2}{7} & = \dfrac{3-2}{7} \\ & = \dfrac{1}{7} \end{aligned} $

2. When denominators are different:

a) Least Common Multiple (LCM) Method:

To Add or Subtract rational numbers through LCM, follow these steps:

Find the LCM of the denominators.
Convert each rational number to an equivalent rational number so that all denominators become equal to the LCM.
Now, add or subtract the numerators and keep the denominator the same.
Simplify the rational number to its standard form (if possible).

Example
Add $\dfrac{3}{4}+\dfrac{5}{6}$
Solution:
$\dfrac{3}{4}+\dfrac{5}{6}$
$\Rightarrow$ First, find the LCM of 4 and 6.
$ \begin{array}{l|rr} 2 & 4,6 \\
\hline 2 & 2,3 \\
\hline 3 & 1,3 \\
\hline & 1,1 \end{array} $
$\Rightarrow$ $2 \times 2 \times 3=12$
$\Rightarrow$ The LCM is 12.
$\Rightarrow$ Make all the denominators same i.e. 12.
$ \begin{aligned} \dfrac{3}{4} & = \dfrac{3 \times 3}{4 \times 3} \\ & = \dfrac{9}{12} \end{aligned} $
$ \begin{aligned} \dfrac{5}{6} & = \dfrac{5 \times 2}{6 \times 2} \\ & = \dfrac{10}{12} \end{aligned} $
$\Rightarrow$ we can write them as:
$ \begin{aligned} \dfrac{3}{4}+\dfrac{5}{6} & = \dfrac{9}{12} + \dfrac{10}{12} \\ & = \dfrac{9+10}{12} \\ & = \dfrac{19}{12} \end{aligned} $

Subtraction:

Subtract $\dfrac{3}{4} – \dfrac{5}{6}$
Solution:
$\dfrac{3}{4} – \dfrac{5}{6}$
$\Rightarrow$ First, find the LCM of 4 and 6.
$ \begin{array}{l|rr} 2 & 4,6 \\ \hline 2 & 2,3 \\ \hline 3 & 1,3 \\ \hline & 1,1 \end{array} $
$\Rightarrow$ $2 \times 2 \times 3=12$
$\Rightarrow$ The LCM is 12.
$\Rightarrow$ Make all the denominators same i.e. 12.
$ \begin{aligned} \dfrac{3}{4} – \dfrac{5}{6} & = \dfrac{3 \times 3}{4 \times 3} – \dfrac{5 \times 2}{6 \times 2} \\ & = \dfrac{9}{12} – \dfrac{10}{12} \\ & = \dfrac{9-10}{12} \\ & = \dfrac{-1}{12} \end{aligned} $

LCM by Long Division Method

Write all denominators in a row.
Divide by the suitable prime number, which divides at least one of the given numbers.
If a number is not divisible, just bring it down.
Continue dividing until all become 1.
Multiply all divisors to get the LCM.

Example:
Find LCM of 4 and 6
$\begin{array}{l|rr}
2 & 4, 6 \\
\hline
2 & 2, 3 \\
\hline
3 & 1, 3 \\
\hline
& 1, 1
\end{array}$
LCM = $ 2 \times 2 \times 3 = 12 $

✅ Tip: Works best for 2 or more denominators.

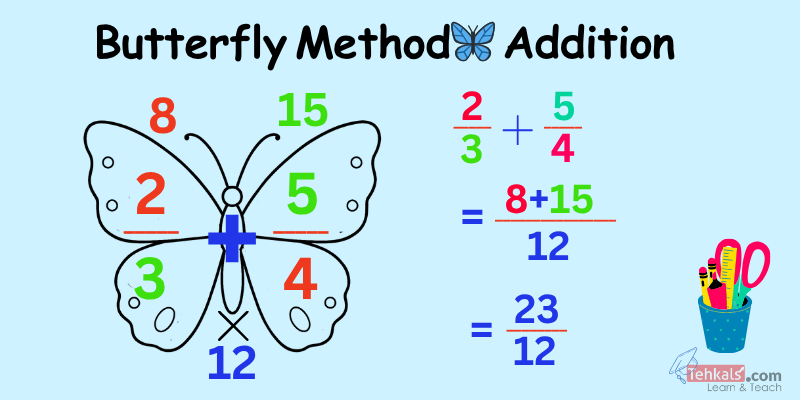
b) Cross Multiplication (Butterfly Method)

This method is also called the butterfly 🦋 method because the multiplication pattern forms crisscross “wings” like a butterfly. It’s a quick way to add two rational numbers with different denominators.

✅ Steps:

Multiply across:
First numerator $\times$ second denominator
Second numerator $\times$ first denominator
Add both results
Multiply the denominators
Write the final fraction and simplify if needed
General Form:
$\dfrac{a}{b} + \dfrac{c}{d}=\dfrac{(a \times d) + (c \times b)}{b \times d}$
Example:
$
\begin{aligned}
\dfrac{2}{3} + \dfrac{5}{4}
&= \dfrac{(2 \times 4) + (5 \times 3)}{3 \times 4} \\
&= \dfrac{8 + 15}{12} \\
&= \dfrac{23}{12}
\end{aligned}
$

Co-Prime Rule

If the denominators have no common factors except 1,
LCM = Product of both denominators.
Example:
LCM of 3 and 4 = $3 \times 4 = 12$

✅ Tip: Great for numbers like 7 & 10, 3 & 8, 11 & 12, etc.

3. Negative Rational Numbers

Use Integers sign rules.
Example 1:
$
\begin{aligned}
\dfrac{-3}{7} + \dfrac{5}{7}
& = \dfrac{-3 + 5}{7} \\
& = \dfrac{2}{7}
\end{aligned}
$
Example 2:
$
\begin{aligned}
\dfrac{-3}{8} + \dfrac{5}{-12}
&= -\dfrac{3}{8} + \left(-\dfrac{5}{12}\right) \\
&= -\dfrac{3}{8} – \dfrac{5}{12} \\
\text{LCM of $8$ and $12$ is $24$} \\
&= -\dfrac{3 \times 3}{8 \times 3} – \dfrac{5 \times 2}{12 \times 2} \\
&= \dfrac{-9}{24} – \dfrac{10}{24} \\
&= \dfrac{-9 – 10}{24} \\
&= \dfrac{-19}{24}
\end{aligned}
$

LCM by Prime Factorization

Find all the prime factors of each denominator.
Find common and non-common prime factors.
$LCM=C.F \times N.C.F$

Example:
Find LCM of 8 and 12
$8 = 2 \times 2\times 2$
$12 = 2 \times 2\times 3$
$LCM=C.F \times N.C.F$
$LCM=2\times 2\times 2\times 3$
LCM $= 24$

✅ Tip: Ideal for clear factorization practice and algebra-based fractions.

4. Whole Number (Integers) & Rational Number

Convert the whole number to a rational number (denominator = 1).
a) Whole Number $\pm$ Rational Number
Example:
$
\begin{aligned}
2 – \dfrac{3}{4}
& = \dfrac{2}{1} – \dfrac{3}{4} \\
& = \dfrac{8}{4} – \dfrac{3}{4} \\
& = \dfrac{8 – 3}{4} \\
& = \dfrac{5}{4}
\end{aligned}
$
b) Rational Number $\pm$ Whole Number
$
\begin{aligned}
\dfrac{11}{5} – 3
&= \dfrac{11}{5} – \dfrac{3}{1} \\
&= \dfrac{11}{5} – \dfrac{15}{5} \\
&= \dfrac{11 – 15}{5} \\
&= \dfrac{-4}{5}
\end{aligned}
$

5. Addition of Mixed Numbers

Convert Mixed Numbers to improper fractions.
Example:
$
\begin{aligned}
1\dfrac{1}{9} – 2\dfrac{2}{3}
&= \dfrac{10}{9} – \dfrac{8}{3} \\
&= \dfrac{10}{9} – \dfrac{8 \times 3}{3 \times 3} \\
&= \dfrac{10}{9} – \dfrac{24}{9} \\
&= \dfrac{10 – 24}{9} \\
&= \dfrac{-14}{9}
\end{aligned}
$

Divisible Rule

If one denominator divides the other, the larger denominator is the LCM.
Example:
LCM of 3 and 9 is 9 because 9 is a multiple of 3.
LCM of (5, 10) is 10

✅ Tip: Saves time — no need for full calculation.

6. Zero in Addition or Subtraction

Adding/subtracting 0 changes nothing.
Example:
$
\begin{aligned}
\dfrac{3}{4} + 0
& = \dfrac{3}{4}
\end{aligned}
$

7. More than Two Rational Numbers

Add or subtract more than two rational numbers, solve step-by-step from left to right, following the same rules for common or different denominators.
a) Example (Same Denominators):
$
\begin{aligned}
\dfrac{3}{7} + \dfrac{2}{7} – \dfrac{4}{7}
& = \dfrac{3 + 2 – 4}{7} \\
& = \dfrac{1}{7}
\end{aligned}
$
b) Example (Different Denominators):
$
\frac{2}{5} + \frac{3}{10} – \frac{1}{4}
$
Step-by-step Solution:
$\begin{aligned}
\dfrac{2}{5} + \dfrac{3}{10} – \dfrac{1}{4}
&= \dfrac{8}{20} + \dfrac{6}{20} – \dfrac{5}{20} \\
&= \dfrac{8 + 6 – 5}{20} \\
&= \dfrac{9}{20}
\end{aligned}
$

Full Example with All Steps Combined

In this example, we’ll simplify a rational number expression that includes negative numbers, fractions, and a mixed number — all in one! We’ll use step-by-step methods like converting to improper fractions, finding the LCM, and simplifying the expression.

Q: Simplify:
$
-3 + \left(-\dfrac{4}{5}\right) + \dfrac{7}{2} – 0 + \left(-1\dfrac{1}{4}\right)
$
✍️ Step-by-step Solution:
Step 1: Convert mixed number to improper fraction:
$
-3 + \left(-\dfrac{4}{5}\right) + \dfrac{7}{2} – 0 + \left(-\dfrac{5}{4}\right)
$
Step 2: Remove brackets:
$
=- \dfrac{3}{1} – \dfrac{4}{5} + \dfrac{7}{2} – \dfrac{5}{4}
$
Step 3: Take LCM of denominators $1, 5, 2, 4$:
$
\begin{array}{l|ccc}
2 & 5, & 2, & 4 \\
\hline
2 & 5, & 1, & 2 \\
\hline
5 & 5, & 1, & 1 \\
\hline & 1, & 1, & 1 \\
\end{array}
$
LCM $= 2 \times 2 \times 5 = \boxed{20}$
Step 4: Convert each number to equivalent rational number with denominator 20:
$
= -\dfrac{60}{20} – \dfrac{16}{20} + \dfrac{70}{20} – \dfrac{25}{20}
$
Step 5: Add/Subtract the fractions:
$
= \dfrac{-60 – 16 + 70 – 25}{20}
$
$
= \dfrac{-31}{20}
$
Step 6: Simplify the fraction:
$
\dfrac{-31}{20} \quad \text{or} \quad -1\dfrac{11}{20}
$

Real-Life Examples

Rational numbers are used in many situations in our daily life. Some real-life examples of rational numbers are given below.

Cooking:
A recipe needs $\dfrac{3}{4}$ cup sugar and $\dfrac{1}{2}$ cup honey.
Total sweetener = $\dfrac{3}{4} + \dfrac{1}{2} = \dfrac{5}{4}$ cups.
Money:
You spend $\dfrac{2}{5}$ of your allowance and then spend $\dfrac{1}{5}$ more.
Total money spent = $\dfrac{3}{5}$ of your allowance.
Temperature:
If the morning temperature is $-2^\circ C$ and it drops by $3^\circ C$,
Final temperature = $-2 – 3 = -5^\circ C$.
Travel:
You walked $\dfrac{3}{4}$ km in the morning and $\dfrac{1}{2}$ km in the evening.
Total distance = $\dfrac{3}{4} + \dfrac{1}{2} = \dfrac{5}{4}$ km.

Common Mistakes to Avoid

Adding denominators instead of finding LCM.
Ignoring negative signs when adding rational numbers.
Forgetting to simplify final answers.
Not converting mixed numbers to improper fractions.

Practice Questions

Try these problems to test yourself:

$\dfrac{3}{8} + \dfrac{1}{8}$
$\dfrac{5}{6} – \dfrac{1}{3}$
$\dfrac{2}{7} + \dfrac{5}{14}$
$-\dfrac{3}{5} + \dfrac{2}{15}$
$1\dfrac{1}{4} + \left(-2\dfrac{3}{8}\right)$

Addition	Subtraction
General Form \( \dfrac{a}{c} + \dfrac{b}{c} = \frac{a+b}{c} \)	General Form \( \frac{a}{c} – \frac{b}{c} = \frac{a-b}{c} \)
Example: \( \begin{aligned} \dfrac{3}{7} + \dfrac{2}{7} & = \dfrac{3+2}{7} \\ & = \dfrac{5}{7} \end{aligned} \)	Example: \( \begin{aligned} \dfrac{3}{7} – \dfrac{2}{7} & = \dfrac{3-2}{7} \\ & = \dfrac{1}{7} \end{aligned} \)