Division of Rational Numbers — Rules, Steps, Real Life Examples and Practice Questions

Division of rational numbers helps us understand how one rational number fits into another. It may seem tricky at first, but with simple methods like reciprocal, KFC, and butterfly, dividing rational numbers becomes easy and fun to learn.

Student Learning Outcomes

By the end of this guide on division of rational numbers, you will be able to:

• Divide any rational numbers, including fractions, integers, mixed numbers, and decimals.
• Use the reciprocal rule and apply the KFC and Butterfly methods correctly.
• Apply sign rules while dividing positive and negative rational numbers.
• Simplify answers and convert results between fraction, mixed, and decimal forms.
• Solve real-life and multi-step division problems with accuracy.

Understanding the Reciprocal

• The reciprocal of a rational number is found by interchanging the numerator and denominator with each other.
  General Form:
  $
  \text{Reciprocal of } \dfrac{a}{b} \text{ is } \frac{b}{a}
  $
  Examples:
• Reciprocal of $\dfrac{3}{4}$ is $\dfrac{4}{3}$
• Reciprocal of $-\dfrac{5}{7}$ is $-\dfrac{7}{5}$
• Zero has no reciprocal.

Dividing Rational Numbers

Dividing rational numbers may look tricky at first, but it’s actually very simple! Instead of dividing directly, we use a neat trick: flip the second fraction (take its reciprocal) and then multiply. After that, just simplify to get the answer in standard form.

Basic Rules

• To divide $\dfrac{a}{b} \div \dfrac{c}{d}$, follow these rules:

1. Find the reciprocal of the second fraction $\dfrac{c}{d} \to \dfrac{d}{c}$
2. Change the division to multiplication.
3. Simplify the rational number to its lowest form, if necessary
4. Multiply numerators together and denominators together.
5. Simplify to Standard Form.
   General Formula:
   $
   \dfrac{a}{b} \div \dfrac{c}{d} = \dfrac{a}{b} \times \dfrac{d}{c}
   $
   Example:
   $
   \begin{aligned}
   \dfrac{5}{7} \div \dfrac{2}{3}
   & = \dfrac{5}{7} \times \dfrac{3}{2} \\
   & = \dfrac{15}{14}
   \end{aligned}
   $

Division of Rational Numbers can also be done by KFC and Butterfly Method.

The KFC Method for Division

The easiest way to divide rational numbers is the KFC method. It stands for:

• K – Keep the first fraction.
• F – Flip the second fraction (take the reciprocal).
• C – Change the division sign to multiplication.
  Example:
  $
  \dfrac{3}{4} \div \dfrac{2}{5}
  $

Step-by-step using KFC Method:

• Keep: $\dfrac{3}{4}$
• Flip: $\dfrac{2}{5} \rightarrow \dfrac{5}{2}$
• Change: $\div \rightarrow \times$
  Now multiply:
  $
  \dfrac{3}{4} \times \dfrac{5}{2} = \dfrac{15}{8}
  $

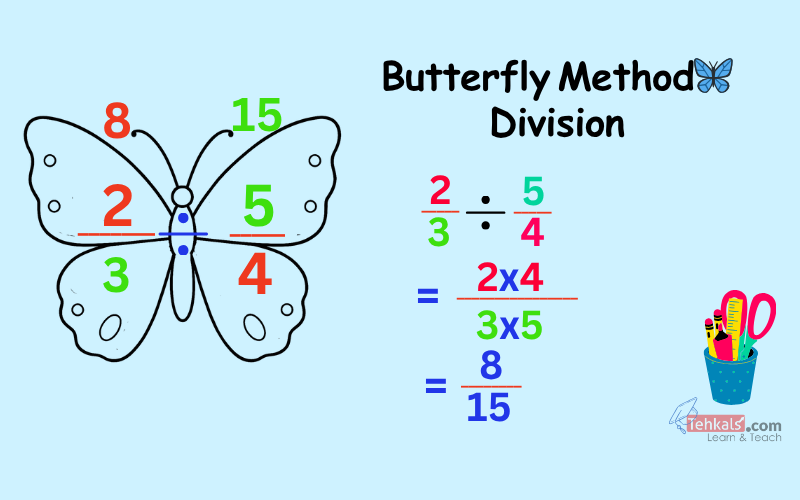
Butterfly Method of Division 🦋

The butterfly method of division is a visual technique for dividing fractions by using crisscross multiplication of rational Numbers.
It looks like the wings of a butterfly.

Different Cases of Division of Rational Numbers

There are different ways to divide rational numbers. Sometimes the numbers are fractions, while other times they are mixed numbers, whole numbers, or decimals. The main idea remains the same as we use the reciprocal, but the steps can change slightly in each case. Let us go through these situations with simple examples to understand them better.

1. Division of Negative Rational Numbers

• To divide negative rational numbers, follow integers sign rules:
  Negative ÷ Negative = Positive
  Positive ÷ Negative = Negative

1. Both are Negative Rational Numbers
   Example:
   $
   \begin{aligned}
   -\dfrac{5}{7} \div -\dfrac{2}{3}
   & = \dfrac{5}{7} \div \dfrac{2}{3} \\
   & = \dfrac{5}{7} \times \dfrac{3}{2} \\
   & = \dfrac{5 \times 3}{7 \times 2} \\
   & = \dfrac{15}{14}
   \end{aligned}
   $
2. One Negative, One Positive Rational Number
   Example:
   $
   \begin{aligned}
   -\dfrac{5}{7} \div \dfrac{2}{3}
   & = -\dfrac{5}{7} \times \dfrac{3}{2} \\
   & = \dfrac{-5 \times 3}{7 \times 2} \\
   & = \dfrac{-15}{14} \\
   & = -\dfrac{15}{14}
   \end{aligned}
   $

2. Division of Rational and Whole (Integers) Numbers

• To divide rational numbers and whole numbers, convert the whole number into a fraction(denominator = 1). \( a = \dfrac{a}{1} \)

1. Divide Fraction by Whole Number
   Example:
   $
   \begin{aligned}
   \dfrac{4}{5} \div 6
   & = \dfrac{4}{5} \div \dfrac{6}{1} \\
   & = \dfrac{4}{5} \times \dfrac{1}{6} \\
   & = \dfrac{\cancel{4}^2}{5} \times \dfrac{1}{\cancel{6}^3} \\
   & = \dfrac{2}{5} \times \dfrac{1}{3} \\
   & = \dfrac{2}{15}
   \end{aligned}
   $
2. Divide Whole Number by Fraction
   Example:
   $
   \begin{aligned}
   6 \div \dfrac{2}{3}
   & = \dfrac{6}{1} \div \dfrac{2}{3} \\
   & = \dfrac{6}{1} \times \dfrac{3}{2} \\
   & = \dfrac{\cancel{6}^3}{1} \times \dfrac{3}{\cancel{2}^1} \\
   & = \dfrac{3}{1} \times \dfrac{3}{1} \\
   & = \dfrac{9}{1} \\
   & = 9
   \end{aligned}
   $

3. Division of Rational and Mixed Numbers

• To divide rational numbers and Mixed numbers, convert the Mixed number into an improper fraction.

1. Divide Fraction by Mixed Number
   Example:
   $
   \begin{aligned}
   \dfrac{2}{5} \div 1\dfrac{1}{2}
   & = \dfrac{2}{5} \div \dfrac{3}{2} \\
   & = \dfrac{2}{5} \times \dfrac{2}{3} \\
   & = \dfrac{4}{15}
   \end{aligned}
   $
2. Divide Mixed Number by Fraction
   Example:
   $
   \begin{aligned}
   2\dfrac{1}{3} \div \dfrac{1}{2}
   & = \dfrac{7}{3} \div \dfrac{1}{2} \\
   & = \dfrac{7}{3} \times \dfrac{2}{1} \\
   & = \dfrac{14}{3}
   \end{aligned}
   $

4. Division of Decimals and Rational Numbers

• To divide rational numbers and Decimals numbers, convert the decimals into fractions, then divide normally.

1. Divide Fraction by Decimal
   Example:
   $
   \begin{aligned}
   \dfrac{3}{4} \div 0.5
   & = \dfrac{3}{4} \div \dfrac{5}{10} \\
   & = \dfrac{3}{4} \times \dfrac{10}{5} \\
   & = \dfrac{3}{4} \times \dfrac{\cancel{10}^2}{\cancel{5}^1} \\
   & = \dfrac{3}{4} \times \dfrac{2}{1} \\
   & = \dfrac{\cancel{6}^3}{\cancel{4}^2} \\
   & = \dfrac{3}{2}
   \end{aligned}
   $
2. Divide Decimal by Fraction
   Example:
   $
   \begin{aligned}
   0.6 \div \dfrac{7}{11}
   & = \dfrac{6}{10} \div \dfrac{7}{11} \\
   & = \dfrac{6}{10} \times \dfrac{11}{7} \\
   & = \dfrac{6 \times 11}{10 \times 7} \\
   & = \dfrac{\cancel{66}^{33}}{\cancel{70}^{35}} \\
   & = \dfrac{33}{35}
   \end{aligned}
   $

5. Division of Two Mixed Numbers

• To divide Two Mixed numbers, convert the both mixed numbers into improper fractions.
  Example:
  $
  \begin{aligned}
  1\dfrac{1}{4} \div 2\dfrac{1}{2}
  & = \dfrac{5}{4} \div \dfrac{5}{2} \\
  & = \dfrac{5}{4} \times \dfrac{2}{5} \\
  & = \dfrac{10}{20} \\
  & = \dfrac{1}{2}
  \end{aligned}
  $

6. Division of Mixed and Whole (Integers) Numbers

• To divide Whole and Mixed numbers, change the mixed number and whole number into fractions before solving.
  Example:
  $
  \begin{aligned}
  3\dfrac{1}{2} \div 2
  & = \dfrac{7}{2} \div \dfrac{2}{1} \\
  & = \dfrac{7}{2} \times \dfrac{1}{2} \\
  & = \dfrac{7}{4}
  \end{aligned}
  $

7. Dividing Fractions (Rational Numbers) with Same Numerators

• If the numerators are the same, divide the second denominator by the first denominator.
  General Form:
  $
  \dfrac{a}{b} \div \dfrac{a}{c} = \dfrac{c}{b}
  $
  Example:
  $
  \dfrac{5}{7} \div \dfrac{5}{9} = \dfrac{9}{7}
  $
  Explanation
  $
  \begin{aligned}
  \dfrac{5}{7} \div \dfrac{5}{9}
  & = \dfrac{5}{7} \times \dfrac{9}{5} \\
  & = \dfrac{\cancel{5}^1}{7} \times \dfrac{9}{\cancel{5}^1} \\
  & = \dfrac{1}{7} \times \dfrac{9}{1} \\
  & = \dfrac{9}{7}
  \end{aligned}
  $

8. Dividing Fractions (Rational Numbers) with Same Denominators

• If the denominators are the same, divide only the numerators (Divide first numerator by second).
  General Form:
  $
  \dfrac{a}{c} \div \dfrac{b}{c} = \dfrac{a}{b}
  $
  Example:
  $
  \dfrac{4}{9} \div \dfrac{5}{9} = \dfrac{4}{5}
  $
  Explanation
  $
  \begin{aligned}
  \dfrac{4}{9} \div \dfrac{5}{9}
  & = \dfrac{4}{9} \times \dfrac{9}{5} \\
  & = \dfrac{4}{\cancel{9}^1} \times \dfrac{\cancel{9}^1}{5} \\
  & = \dfrac{4}{5}
  \end{aligned}
  $

9. Division of Same Rational Numbers

• Any number divided by itself is always equal to 1.
  Example:
  $
  \dfrac{7}{8} \div \dfrac{7}{8} = 1
  $
  Explanation
  $
  \begin{aligned}
  \dfrac{7}{8} \div \dfrac{7}{8}
  & = \dfrac{7}{8} \times \dfrac{8}{7} \\
  & = \dfrac{\cancel{7}^1}{\cancel{8}^1} \times \dfrac{\cancel{8}^1}{\cancel{7}^1} \\
  & = 1
  \end{aligned}
  $

10. Division of Zero and Rational Numbers

• Zero divided by any number is 0, but dividing by 0 is undefined.

1. Zero Divided by Rational Number
   $0 \div \text{any number} = 0$
   Example:
   $
   0 \div \dfrac{5}{6} = 0
   $
2. Rational Number Divided by Zero
   $\text{Any number} \div 0$ is undefined
   Example:
   $
   \dfrac{3}{4} \div 0 = \text{undefined}
   $

11. Division by the Reciprocal of a Rational Number

• To divide a rational number by its reciprocal, gives the square of that numbers.
  Example:
  $
  \dfrac{2}{3} \div \dfrac{3}{2}
  = \dfrac{4}{9}
  $
  Explanation:
  $
  \begin{aligned}
  \dfrac{2}{3} \div \dfrac{3}{2}
  & = \dfrac{2}{3} \times \dfrac{2}{3} \\
  & = \dfrac{2 \times 2}{3 \times 3} \\
  & = \dfrac{4}{9}
  \end{aligned}
  $

Quick Tips for Division of Rational Numbers

• Always change division into multiplication by using the reciprocal of the second number.
• Divide: $\dfrac{a}{b} \div \dfrac{c}{d} = \dfrac{a}{b} \times \dfrac{d}{c}$
• Simplify before and after dividing to keep numbers small.
• Follow the same sign rules:
  Negative ÷ Negative = Positive
  Positive ÷ Negative = Negative
• Convert mixed numbers and decimals into fractions before dividing.
• Write whole numbers as $\dfrac{a}{1}$ when dividing.
• Use cross-cancellation after changing to multiplication.
• Use brackets around negative numbers to avoid sign confusion.

Practice Questions

Practice Question # 1
$-2 \div \dfrac{3}{5} \div 4\dfrac{1}{2} \div \left(-\dfrac{10}{9}\right)$
Solution:

1. Convert the mixed number to an improper fraction
   $4\dfrac{1}{2} = \dfrac{9}{2}$
2. Rewrite the expression using fractions
   $= \dfrac{-2}{1} \div \dfrac{3}{5} \div \dfrac{9}{2} \div \left(-\dfrac{10}{9}\right)$
3. Convert divisions to multiplications by reciprocals
   $= \dfrac{-2}{1} \times \dfrac{5}{3} \times \dfrac{2}{9} \times \left(-\dfrac{9}{10}\right)$
   $= \dfrac{-2}{1} \times \dfrac{5}{3} \times \dfrac{2}{9} \times \dfrac{-9}{10}$
4. Cancel common factors step by step
   Cancel (9) in numerator with (9) in denominator.
   Cancel (5) in numerator with (10) in denominator.
   $= \dfrac{-2}{1} \times \dfrac{1}{3} \times \dfrac{2}{1} \times \dfrac{-1}{2}$
   Now again cancel (2) in numerator with (2) in denominator.
   $= \dfrac{-2}{1} \times \dfrac{1}{3} \times \dfrac{1}{1} \times \dfrac{-1}{1}$
5. Multiply numerators and denominators
   $= \dfrac{-2 \times 1 \times 1 \times (-1)}{1 \times 3 \times 1 \times 1}$
   $= \dfrac{2}{3}$

Practice Question # 2
$\dfrac{-3}{4} \div 2\dfrac{1}{2} \div \dfrac{5}{6} \div 0.8$
Solution:

1. Convert mixed and decimal numbers to fractions
   $2\dfrac{1}{2} = \dfrac{5}{2}, \quad 0.8 = \dfrac{8}{10}$
2. Rewrite the expression using fractions
   $\dfrac{-3}{4} \div \dfrac{5}{2} \div \dfrac{5}{6} \div \dfrac{8}{10}$
3. Change all divisions to multiplications by reciprocals
   $\dfrac{-3}{4} \times \dfrac{2}{5} \times \dfrac{6}{5} \times \dfrac{10}{8}$
4. Cancel common factors step by step
   Cancel (4) in denominator with (2) in numerator.
   Cancel (6) in numerator with (8) in denominator.
   Cancel (5) in denominator with (10) in numerator.
   $\dfrac{-3}{2} \times \dfrac{1}{5} \times \dfrac{3}{1} \times \dfrac{2}{4}$
   Now cancel (2) in numerator with (4) in denominator.
   $\dfrac{-3}{2} \times \dfrac{1}{5} \times \dfrac{3}{1} \times \dfrac{1}{2}$
5. Multiply numerators and denominators
   $= \dfrac{-3 \times 1 \times 3 \times 1}{2 \times 5 \times 1 \times 2}$
   Negative ÷ Positive = Negative
   $= \dfrac{-9}{20}$
   $= -\dfrac{9}{20}$

Practice Question # 3
$4\dfrac{1}{5} \div \left(-\dfrac{3}{7}\right) \div 0.6 \div \dfrac{-7}{5}$
Solution:

1. Convert mixed and decimal numbers to fractions
   $4\dfrac{1}{5} = \dfrac{21}{5}, \quad 0.6 = \dfrac{6}{10}$
2. Rewrite the expression using fractions
   $\dfrac{21}{5} \div \left(-\dfrac{3}{7}\right) \div \dfrac{6}{10} \div \dfrac{-7}{5}$
3. Change all divisions to multiplications by reciprocals
   $\dfrac{21}{5} \times \left(-\dfrac{7}{3}\right) \times \dfrac{10}{6} \times \left(-\dfrac{5}{7}\right)$
4. Cancel common factors step by step
   Cancel (21) in numerator with (3) in denominator.
   Cancel (5) in numerator with (5) in denominator.
   Cancel (7) in numerator with (7) in denominator.
   Cancel (6) in denominator with (10) in numerator.
   $\dfrac{7}{1} \times \dfrac{-1}{1} \times \dfrac{5}{3} \times \dfrac{-1}{1}$
5. Multiply numerators and denominators
   $= \dfrac{7 \times -1 \times 5 \times -1}{1 \times 1 \times 3 \times 1}$
   Now simplify the signs:
   Negative × Negative = Positive
   $= \dfrac{35}{3}$
6. Convert to Mixed Number
   $= 11\dfrac{2}{3}$

Previous Post

Multiplying Rational Numbers – Rules, Real Life Examples, and Practice Questions

---

Next Post

Mathematics notes for class 10 PDF (KPK)

Latest Posts

Division of Rational Numbers — Rules, Steps, Real Life Examples and Practice Questions

---

29 Oct 2025

95

Multiplying Rational Numbers – Rules, Real Life Examples, and Practice Questions

---

29 Oct 2025

109

Addition and Subtraction of Rational Numbers – Easy and Step-by-Step Rules with Examples

---

17 Oct 2025

42

Please Write Your Comments

Comments (0)

Leave your comment.

Add Comment +

INSTRUCTIONS:

• Be Respectful
• Stay Relevant
• Stay Positive
• True Feedback
• Encourage Discussion
• Avoid Spamming
• No Fake News
• Don't Copy-Paste
• No Personal Attacks