Understanding Integer Properties: A Beginner’s Guide with Real-Life Examples, Worksheets & MCQs

Published: 4 Oct 2025

Confused 🤔about integer rules ? Don’t worry 😥, you’re not alone! This easy guide explains the basic Properties of Integers—like closure, commutative, associative, and distributive—in simple steps with real-life examples. You can also practice with free downloadable worksheets and interactive MCQs designed specifically for Grades 6-8. Let’s turn confusion into clear understanding—ready to get started?🚀

Table of Content

Properties of Integers

Properties of Integers

🤔Properties of integers are the basic rules that show how numbers work together. For example, adding two integers always gives another integer—this is known as the closure property. Other simple rules, like the commutative, associative, and distributive properties, help keep math predictable and easy to understand.

Closure Property of Integers

Closure Property of Addition
The sum of integers is always an integer.
Statement:
$ a+b=Z $
Example:
$ 3+8=11 $
Where $ 11 $ is an Integer.
Closure Property of Subtraction
The difference of integers is always an integer.
Statement:
$ a-b={ Z } $
Example:
$ 3-8=-5 { \ (Z) } $
Closure Property of Multiplication
The product of integers is always an integer.
Statement:
$ a \times b= { Z } $
Example:
$ 3 \times 8=24 \ \ (Z) $
$ -3 \times 8=-24 \ \ { (Z) } $
Closure Property of Division
The division of two integers may or may not be an integer.
Statement:
$ a \div b= Z $ (Exactly divisible)
$ a \div b \neq Z $ (Not exactly divisible)
Example:
$ -12 \div 4=-3 \ { (Z) } $
$ 9 \div 2=4.5 \ (Not \ an \ Integer) $

Closure Property of Integers Worksheet

Download Closure Property of Integers Worksheet

Download Worksheet

Commutative Property of Integers

Commutative Property of Addition:
When we change the position or order of two integers in addition does not change the final result.
Statement:
If $ a, b \in Z $ then $ a+b= b+a$
Example:
$ -7+9=9+(-7) $
$ -7+9=9-7 $
$ 2=2 $
Commutative Property of Multiplication
When we change the position or order of two integers in multiplication does not change the final result.
Statement:
If $ a, b \in Z $ then $ a . b= b.a $
Example:
$ 7 \times 9=9 \times 7 $
$ 63=63 $

No Commutative Property for Subtraction and Division

Commutative Property of Subtraction and Division may not be applicable.
Examples:
3. Commutative Property of Subtraction
$ 7-9=9-7 $
$ -2 \neq 2 $

4. Commutative Property of Division
$\frac{6}{3} \neq \frac{3}{6} $
$ 2 \neq 0.5 $

Commutative Property of Integers Worksheet

Download Commutative Property of Integers Worksheet

Download Worksheet

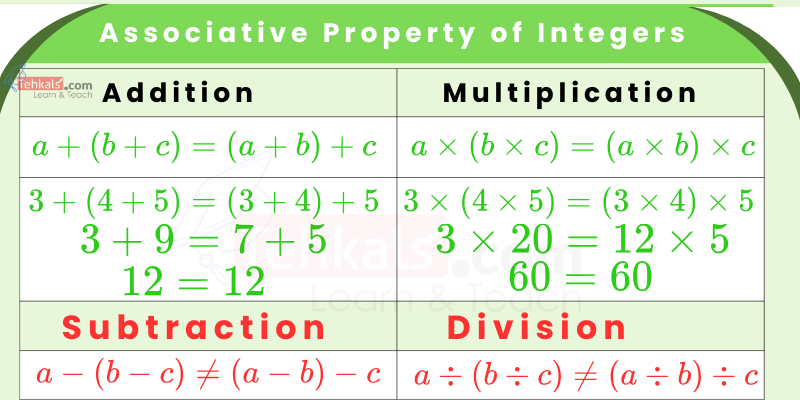
Associative Property of Integers

Associative Property of Addition:
The order of grouping the integers in different ways in Adding does not affect the final result.
Statement:
If $ a, b, c \in Z $ then
$ a+(b+c)=(a+b)+c $
Example:
$ 3+(4+5) =(3+4)+5 $
$ 3+9 =7+5 $
$ 12 =12 $
Associative Property of Multiplication
The order of grouping the integers in different ways in Multiplying does not affect the final result.
Statement:
If $ a, b, c \in Z $ then
$ a(b c)=(a b) c $
OR
$ a \times(b \times c)=(a \times b) \times c $
Example:
$ 3 \times(4 \times 5)=(3 \times 4) \times 5 $
$ 3 \times 20=12 \times 5 $
$ 60=60 $

No Associative Property for Subtraction and Division

Associative Property of Subtraction and Division may not be applicable.
Examples:
3. Associative Property of Subtraction
$ 2-(3-5) =(2-3)-5 $
$ 2-(-2) =(-1)-5 $
$ 2+2 =-1-5 $
$ 4 \neq-6 $

4. Associative Property of Division
$ 2 \div(3 \div 5)=(2 \div 3) \div 5 $
$ 2 \div 0.6=0.66 \div 5 $
$ 3.333 \ldots \neq 0.132 $

Associative Property of Integers Worksheet

Download Associative Property of Integers Worksheet

Download Worksheet

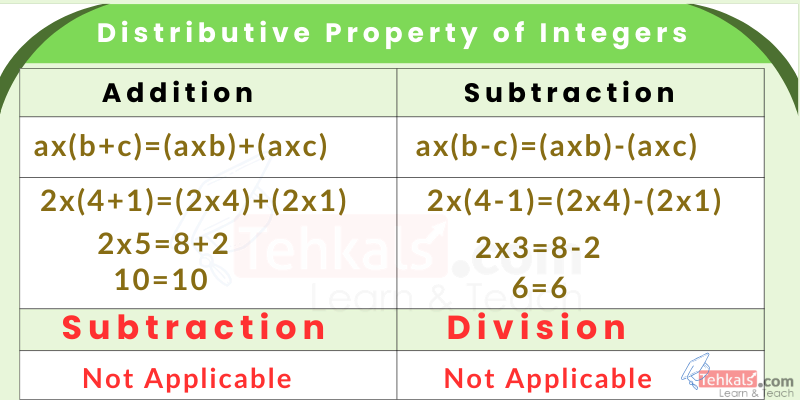
Distributive Property of Integers

Distributive Property over Addition:
The distributive property of integers over addition states that multiplying an integer by the sum of two integers is the same as multiplying the integers separately and then adding the products.
Statement:
$ a \times(b+c)=(a \times b)+(a \times c) $
Example:
$ 2 \times(4+1)=(2 \times 4)+(2 \times 1) $
$ 2 \times 5=8+2 $
$ 10=10 $
Distributive Property over Subtraction:
The distributive property of integers over subtraction states that multiplying an integer by the difference of two integers is same as multiplying the integers separately and then subtracting the products.
Statement:
$ a \times(b-c)=(a \times b)-(a \times c) $
Example:
$ 2 \times(4-1)= (2 \times 4)-(2 \times 1) $
$ 2 \times 3=8-2 $
$ 6=6 $

Distributive Property of Integers Worksheet

Download Distributive Property of Integers Worksheet

Download Worksheet

Additive and Multiplicative Identity

Identity elements are special numbers that keep a number unchanged during an operation. In addition, 0 is the additive identity because adding 0 to any integer does not change its value. In multiplication, 1 is the multiplicative identity because multiplying any integer by 1 keeps it the same.

Additive Identity of Integers

Zero (0) is called Additive Identity because adding “0” to any integer does not change that integer.
Statement:
$ a+0=0+a=a $
Examples:

$ 3+0=0+3=3 $
If we add $3$ and $0$, we get $3$.
$ -5+0=-5 $
$ 9+0=9 $

The Magic of Zero in Addition and Subtraction

When any integer is added to or subtracted from $0$, the result is the integer itself.
Examples:

$a + 0 = a$
$a – 0 = a$

Multiplicative Identity of Integers

1 is called Multiplicative Identity because multiplying “1” to any integer does not change that integer.
Statement:
$ a \times 1=1 \times a=a $
Examples:

$ 3 \times 1=1 \times 3=3 $
If we add $3$ and $0$, we get $3$.
$ -5 \times 1=-5 $
$ 9 \times 1=9 $

Understanding Opposites and Reciprocals in Math

The opposite of $2$ is $-2$.
The opposite of $-2$ is $2$.
The reciprocal of $3$ is $\frac{1}{3}$.
The reciprocal of $\frac{1}{3}$ is $3$.

Additive and Multiplicative Identity Worksheet

Download Additive and Multiplicative Identity Worksheet

Download Worksheet

Additive and Multiplicative Inverse

An additive inverse of a number is the value that gives zero when added to it. For example, the additive inverse of $ +7 $ is $ -7 $. A multiplicative inverse (also called reciprocal) is the value that gives 1 when multiplied with the number. For example, the multiplicative inverse of $ 5 $ is $ \frac{1}{5} $.

Additive Inverse of Integers

If we add an integer to its opposite integer, the result will always be zero $(0)$.
If $ a \in Integer $ then $ a+a^{\prime}= a^{\prime}+a=0$ then $ a^{\prime} $ is called additive inverse of $ a $
Statement:
$ a+(-a)=-a+a=0 $
$ 10+(-10)=-10+10=0 $
Examples:

$ 3+(-3)=0 $
$ -5+5=5-5=0 $
$ -20+20=0 $
$ 10-10=0 $
$ a+(-a)=0 $

Multiplicative Inverse of Integers

If we multiply an integer to its reciprocal integer, the result will always be $“1”$.
If $ a \in Integr $ then $ a \cdot a^{-1}= a^{-1} \cdot a=1 $ then $ a^{-1} $ is called multiplicative inverse of $ a $ .
Statement:
$ a \cdot \frac{1}{a}=\frac{1}{a} \cdot a=1 $
$ 10. \frac{1}{10}=\frac{1}{10} \cdot 10=1 $
Examples:

$ 5 . \frac{1}{5}=1 $
$ -3 \times \frac{1}{-3}=1 $
$ -3\left(\frac{1}{-3}\right)=1 $

Additive and Multiplicative Inverse Worksheet

Download Additive and Multiplicative Inverse Worksheet

Download Worksheet