How to Compare and Order Integers: A Step-by-Step Guide with Examples, Worksheets & MCQs

Published: 30 Sep 2025

Welcome to our guide on ordering and comparing integers! In this post, you’ll learn how to use number lines and real-life examples to easily figure out how integers line up and relate to each other. With clear steps, free downloadable worksheets, and fun MCQs for Grades 6-8, you’ll quickly master these essential math skills. Let’s get started!

Table of Content

Absolute or Numerical value of an Integer
1. Absolute value of an Integer Worksheet
Represent Integers on a Number Line
1. Integers on a Number Line Worksheet
Ordering and Comparing Integers on a Number Line
1. Ordering Integers on a Number Line Worksheet
Comparing and Ordering of Integers
1. Comparing of Integers Worksheet

Absolute or Numerical value of an Integer

Absolute or Numerical value is the value of integers which is measured from $ 0 $. Absolute value is denoted by vertical bars by using the symbol $| \ \ | $.

The absolute or numerical value of any integer (positive or negative) is always positive.

The absolute value of $ |+10| $ is $ 10 $ .
The absolute value of $ |-10 | $ is $ 10 $ .
The absolute value of $ |0 | $ is $ 0 $ .

Note:
The distance of $10$ and $-10$ is same from $0$ but in opposite directions.

Numerical or Absolute Value

The numerical value or absolute value of the same positive or negative numbers is equal.
The numerical value of $ +7 $ and $ -7 $ is equal which is $ ‘7’ $

Feature of Integers
Integers have two features:

Numerical Value
Signs $ (+, -) $

Numerical value is the value of integers measured from “$0$”.
The sign $+ $ or $- $ with Numerical Value shows the direction relative to zero.

$ \spadesuit +37 {\ ^oC} $ shows high temperature (Hotness).
$ \spadesuit -5 {\ ^oC} $ shows low temperature (Coldness).

Absolute value of an Integer Worksheet

Download Absolute value of an Integer Worksheet for free

Download Worksheet

Represent Integers on a Number Line

The arrows on both sides indicated that positive and negative integers keep counting.
Positive integers are to the right of zero.
Negative integers are to the left of zero.

Note:

The distance between any two points on the number line is always same or equal.
Positive and Negative integers are represented on the number line in opposite direction.

Integers on a Number Line Worksheet

Download Number Line Worksheet for free

Download Worksheet

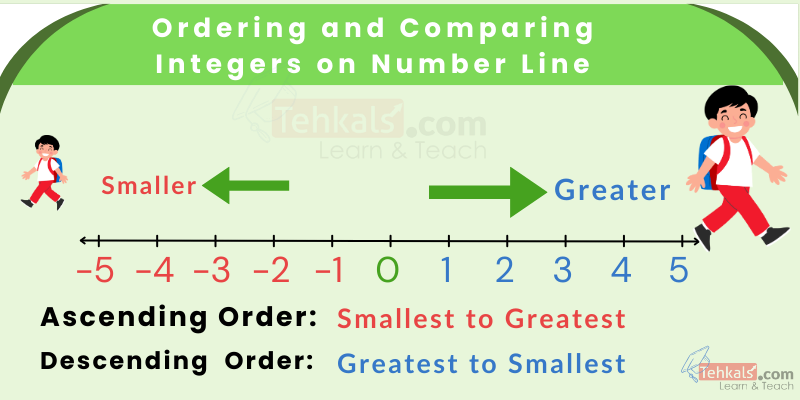
Ordering and Comparing Integers on a Number Line

On a number line, the values of integers increase in the right direction and decrease in the left direction.
On a number line, zero is greater than all integers to the left and smaller than all integers to the right.
On a number line, the integers to the right of “0” are greater than those to the left of “0”.
On a number line, zero separates positive and negative integers.

Greater, Smaller, and Consecutive Numbers

On a number line, each number is smaller than all the numbers to its right and greater than all the numbers to its left.
$5>3$ means $5$ is greater than $3$.
$6<9$ means $6$ is smaller than $9$.

“Numbers that are next to each other in counting are called consecutive numbers.”
For example: $ 1, 2, 3 $ or $ -3, -2, -1 $

Example:
Which is greater $ -10 \ or \ 3 $ ?
Solution:
On the number line, $ -10 $ lies to the left of $ 3 $.
So, $ 3 $ is greater than $ -10 $.

Ascending and Descending Order

Definitions:

Ascending Order: Arrangement of numbers from smallest to greatest.
Descending Order: Arrangement of numbers from greatest to smallest.

Ordering Integers on a Number Line Worksheet

Download Ordering Integers on a Number Line Worksheet for free

Download Worksheet

Comparing and Ordering of Integers

Positive integers (e.g. $1, 2, 3$) are always greater than negative integers (e.g. $-1, -2, -3$).
For positive integers, the larger value is always greater (e.g. $5 > 3$).
For negative integers, the smaller value is always greater (e.g.$-3 > -5$ ).
Zero $0$ is greater than all negative integers and smaller than all positive integers.

Example:
Which is smaller $ -5 \ or -9 $.
Solution:
Here, both the integers have negative signs. Thus, the largest integer is smaller. So $ -9 $ is smaller than $ -5 $

$ Arrange \ -8,9,-9,8,0,5,-5,6 $ in ascending and descending order.

$ -8,9,-9,8,0,5,-5,6 $
Step 1: Separate Positive, Negative, and Zero Integers
Positive integers: $9, 8, 5, 6$
Negative integers: $-8, -9, -5$
Zero: $0$

Step 2: Order Each Group
Integers having positive signs, the greater integer is always greater.
$ 9>8>6>5 $
Integers having negative signs, then the smallest integer is greater.
$ -5>-8>-9 $
$0$ is smaller than the positive and greater than the negative integers. Thus, it lies between them.

Step 3: Ascending and Descending Order
Ascending Order: $ -9, -8, -5, 0, 5, 6, 8, 9 $
Descending Order: $ 9,8,6,5,0,-5,-8,-9 $

Comparing of Integers Worksheet

Download Ordering Integers on a Number Line Worksheet for free

Download Worksheet