What is a Rational Number? Definition, Types, Practical Examples, Comparing, Ordering & Representation of Rational Number on Number Line.
Published: 12 Oct 2025
When we hear the term “number,” various types may come to mind—integers, decimals, fractions, and more. One important category among these is Rational Number. But what exactly is a rational number? This blog will explore rational numbers in detail, explaining their types and providing clear examples to make the concept easy to understand.
Introduction to Rational Numbers
In mathematics, when one integer is divided by another, the result may or may not be an integer.
- Dividing \(-14\) by \(2\) gives the integer \(-7\).
- Dividing \(-15\) by \(2\) gives \(\dfrac{-15}{2}\), which cannot be simplified further into an integer.
Numbers like \(\dfrac{-15}{2}\), which can be expressed as the ratio of two integers. thus, mathematicians introduced the concept of Rational Numbers.
What is a Rational Number?
Rational numbers are real numbers that can be written as a fraction, where both the numerator and denominator are integers, and the denominator is not zero. This includes whole numbers, integers, fractions, and decimals that either terminate or repeat.
Meaning of Rational Number
The word “rational” comes from the Latin word “ratio,” meaning a relationship between two numbers. Rational numbers are like fractions that represent these ratios, where both the numerator and denominator are integers.
How to Write Rational Numbers
A rational number can be written by dividing one integer by another integer. All numbers in the rational number set can be expressed as a ratio of two integers.
The set of rational numbers is a superset of the set of integers because every integer can be written as a rational number.
Definition of Rational Numbers
A rational number is any number that can be expressed as the quotient or fraction of two integers in the form \(\dfrac{p}{q}\), where \(q \neq 0\).
Mathematically:
\( \text{Rational number} = \dfrac{p}{q} \)
\( \text{ where } p, q \in \mathbb{Z} \text{ and } q \neq 0. \)

Set of Rational Numbers
The set of rational numbers includes natural numbers, whole numbers, integers, fractions, and both terminating and repeating decimals.
\[
Q = \left\{ \frac{p}{q} \;\middle|\; p, q \in \mathbb{Z}, \; q \neq 0 \right\}
\]
A rational number is denoted by the symbol \(Q\), which comes from the word “Quotient.”
Examples of Rational Numbers:
- Fractions: \( \dfrac{2}{3}, \quad \dfrac{-5}{8} \)
- Integers: \( -4 \) (which can be written as \( \dfrac{-4}{1} \))
- Terminating decimals: \( 0.5, \quad 2.75 \)
- Repeating decimals: \( 0.\overline{3}, \quad 1.\overline{6} \)
Daily Life Examples of Rational Numbers
- Fractions
When you drink half a glass of water, you consume \(\dfrac{1}{2}\) of the glass.
If you cut a cake into 4 equal pieces and eat one, you have eaten \(\dfrac{1}{4}\) of the cake. - Integers
A building with 5 floors above and 2 floors underground can be represented as +5 and -2 respectively.
If the temperature is -3°C, it is a rational number because it can be written as \(\dfrac{-3}{1}\). - Terminating Decimals
The price of a product like $4.75 is a terminating decimal because it can be written as \(\dfrac{475}{100}\).
A 2.5-liter bottle of water represents a rational number since it can be expressed as \(\dfrac{25}{10}\). - Repeating Decimals
If a car consumes \( \dfrac{1}{3} \) liters of fuel per kilometer, it means the fuel efficiency is $0.333\ldots$ or \( 0.\overline{3} \) liters per km.
If a cyclist rides \( \dfrac{10}{3} \) km in an hour, the speed is 3.333… km/h.

Positive and Negative Rational Numbers
| Positive Rational Numbers | Negative Rational Numbers |
|---|---|
| The numerator and denominator both have the same sign. | The numerator and denominator have opposite signs. |
| Positive rational numbers are always greater than 0. | Negative rational numbers are always less than 0. |
| General Form: \( \dfrac{p}{q}\), \( \dfrac{-p}{-q}\) | General Form: \( \dfrac{-p}{q}\), \( \dfrac{p}{-q}\) |
| Examples: \( \dfrac{11}{7}\), \( \dfrac{-11}{-7}\) | Examples: \( \dfrac{-11}{7}\), \( \dfrac{11}{-7}\) |
Standard form of a Rational Number
A rational number is in standard form if:
- The numerator and denominator have no common factors other than 1.
- The denominator is positive.
Example:
Convert \(\dfrac{15}{-35} \) to its standard form:
Solution:
\(\dfrac{15}{-35}=-\dfrac{3}{7} \)
Thus, \(-\dfrac{3}{7} \) is in standard form because it has no common factor and the denominator is also positive.
🌟Types of Rational Numbers🌟
There are 5 types of rational numbers you see every day. Let’s take a quick look at each one and explore them with examples!
- Fractions in the form of \(\dfrac{p}{q}\), where $p$ & $q$ are integers and \(q \neq 0\), are rational numbers.
Examples:
\( \dfrac{8}{-3}, -\dfrac{6}{11} \) - Natural, Whole numbers and integers can be written as rational numbers with a denominator of \(1\).
Examples:
\(5\): Expressed as \(\dfrac{5}{1}\)
\(-6\): Expressed as \(\dfrac{-6}{1}\) - Zero can be written as a rational number with any non-zero denominator.
Examples:
\(0\): Expressed as \(\dfrac{0}{1}, \dfrac{0}{7}, \dfrac{0}{-5}\) - Perfect roots of numbers are rational numbers if they simplify to integers.
Examples:
\(\sqrt{25} = 5 = \dfrac{5}{1}\)
\(\sqrt[3]{27} = 3 = \dfrac{3}{1}\)
\(\sqrt[4]{256} = 4 = \dfrac{4}{1}\)
\(\sqrt[6]{64} = 2 = \dfrac{2}{1}\) - Terminating and repeating decimals can also be written as rational numbers.
Examples:
\(0.111 \)
\(-0.19 \)
\(3.333\ldots \)

Mixed into Improper Fraction
Multiply the whole number by the denominator of the fraction and then add to the numerator.
Example:
Convert \( 3 \dfrac{2}{5} \) to an improper fraction:
\( 3 \dfrac{2}{5} = \dfrac{(3 \times 5) + 2}{5} \)
\( 3 \dfrac{2}{5} = \dfrac{15 + 2}{5} \)
\( 3 \dfrac{2}{5} = \dfrac{17}{5} \)
Improper into Mixed Fraction:

Representation of Rational Numbers on Number Line
Rational numbers can be written as fractions or decimals, and they can be shown on a number line just like whole numbers.
There are two common ways to do this:
1. Successive Magnification (Decimal Method):
Change the fraction into a decimal and then find its place on the number line by dividing the gap between two numbers into smaller parts (like tenths or hundredths).
Steps
- Convert the fraction into decimal form.
$\dfrac{p}{q} =$ decimal value. - Check the sign.
If it is positive, the point lies on the right side of zero.
If it is negative, the point lies on the left side of zero. - Draw a number line.
Mark integers clearly: $-3, -2, -1, 0, 1, 2, 3$. - Locate the integer interval
Mark the integer part of the decimal as the starting point.
The rational number lies between this and next integer. - Subdivide the relevant interval.
Divide the section between the integers into smaller parts depending on the decimal scale. - Locate the decimal value.
Place a point at the approximate position of the decimal value. - Mark and label the point.
Label it with the original rational number or its decimal equivalent.
Note:
The process for plotting rational numbers on the number line is similar to plotting integers, but it requires attention to the decimal point for accurate placement.
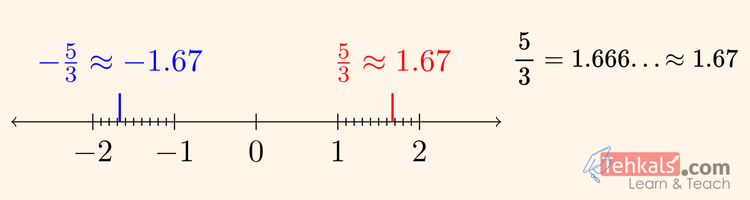
Example
Represent the following rational numbers on number line.
$\dfrac{5}{3}$ and $-\dfrac{5}{3}$
- Convert the fraction into decimal form.
$
\dfrac{5}{3} = 1.666\ldots \approx 1.67
$
$
-\dfrac{5}{3} = -1.666\ldots \approx -1.67
$ - Check the sign.
$\dfrac{5}{3}$ is positive → right of zero.
$-\dfrac{5}{3}$ is negative → left of zero. - Draw a number line.
Mark integers clearly: $-3, -2, -1, 0, 1, 2, 3$. - Locate the integer interval
$1$ and $-1$ are the starting points.
The two consecutive integers are:
$(-1 \ \& \ -2)$ and $(1 \ \& \ 2)$. - Subdivide the relevant interval.
Split each interval into 10 equal parts. - Locate the decimal value.
$ 1.67 $ lies between 1.6 and 1.7, closer to $1.7$.
$ -1.67 $ lies between -1.6 and -1.7, closer to $-1.7$. - Mark and label the point.
Label them as:
$\dfrac{5}{3} \ (or \ 1.67)$
$-\dfrac{5}{3} \ (or \ -1.67)$ .
2. Fraction Subdivision Method:
Divide the space between two numbers into equal parts based on the denominator of the fraction and then count the parts to mark the number.
Steps:
- Write the rational number in fraction form.
Ensure it is in the form $\dfrac{p}{q}$.
Convert improper fraction to mixed number if necessary. - Check the sign.
If positive → point lies on the right side of zero.
If negative → point lies on the left side of zero. - Draw a number line.
Mark integers clearly: $-3, -2, -1, 0, 1, 2, 3$. - Locate the integer interval.
Identify the whole-number part of the rational number.
The number lies between this integer and the next consecutive integer. - Divide the interval into equal parts based on the denominator.
If the denominator is 4 → divide each unit interval into 4 equal parts.
If the denominator is 3 → divide each unit into 3 equal parts, and so on. - Count the steps.
Count $p$ based on the denominator $\dfrac{1}{q}$.
If $p$ is positive → move right.
If $p$ is negative → move left. - Mark and label the point.
Place a dot at the correct position and label it with the rational number (fraction or mixed number).
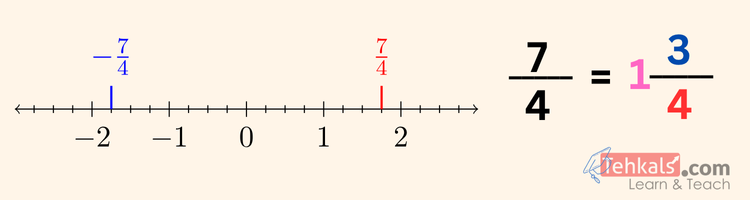
Example:
Plot $\dfrac{7}{4}$ and $-\dfrac{7}{4}$
- Write the rational number in fraction form.
$\dfrac{7}{4}, \quad -\dfrac{7}{4}$
Convert to mixed numbers:
$\dfrac{7}{4} = 1 \dfrac{3}{4}, \quad -\dfrac{7}{4} = -1 \dfrac{3}{4}$ - Check the sign.
$\dfrac{7}{4}$ is positive → right of zero.
$-\dfrac{7}{4}$ is negative → left of zero. - Draw a number line.
Mark integers clearly: $-3, -2, -1, 0, 1, 2, 3$. - Locate the integer interval.
$1 \dfrac{3}{4}$ lies between $1$ and $2$.
$-1 \dfrac{3}{4}$ lies between $-2$ and $-1$. - Divide the interval into equal parts based on the denominator.
Denominator = $4$ → divide each unit interval into 4 equal parts. - Count the steps.
From $1$, count 3 steps of size $\dfrac{1}{4}$ → reach $1 \dfrac{3}{4}$.
From $-1$, count 3 steps of size $\dfrac{1}{4}$ to the left → reach $-1 \dfrac{3}{4}$. - Mark and label the point.
Mark $\dfrac{7}{4}$ at $1 \dfrac{3}{4}$.
Mark $-\dfrac{7}{4}$ at $-1 \dfrac{3}{4}$.
- \(>\) means greater than
- \(<\) means less than
- \( \geq \) means greater than or equal to
- \( \leq \) means less than or equal to
- Ascending Order: Arrangement of numbers from smallest to greatest.
- Descending Order: Arrangement of numbers from greatest to smallest.
- Positive vs Negative Rational Numbers
Every positive rational number is always greater than any negative rational number and also greater than zero.
Example:
\(\dfrac{7}{4}\) is greater than both \(-\dfrac{11}{6}\) and \(0\). - Among positive rational numbers, the larger value is always greater.
Example:
Between \(\dfrac{3}{4}\) and \(\dfrac{5}{4}\):
\(\frac{5}{4}\) is greater than \(\dfrac{3}{4}\), because \(5 > 3\) when comparing numerators (denominators are the same). - Among negative rational numbers, the smaller value is greater.
Example:
Between \(-\dfrac{3}{4}\) and \(-\dfrac{5}{4}\):
\(-\dfrac{3}{4}\) is greater than \(-\dfrac{5}{4}\),
Comparing Rational Numbers
Comparing rational numbers means finding out which number is greater, smaller, or if they are equal.
Same Denominators:
- If the denominators of the rational numbers are the same, the rational number with the greater numerator is larger.
Example:
Compare \(\dfrac{6}{7}\) and \(\dfrac{4}{7}\)
Solution:
\(\dfrac{6}{7}\) and \(\dfrac{4}{7}\)
As the denominators are same.
Compare their numerators. So \(6 > 4\)
Therefore:
\(\dfrac{6}{7} > \dfrac{4}{7} \)
Different Denominators:
If the denominators are different, follow the following steps.
- Find the least common multiple (LCM) of the denominators.
- Multiply all rational numbers by a number so that their denominators become equal to their LCM.
- Compare the numerators to determine which is greater.
Example:
Compare $-\dfrac{5}{6}$ and $-\dfrac{3}{8}$:
Solution
\(-\dfrac{5}{6}\) and \(-\dfrac{3}{8}\)
- First find a common denominator by taking LCM.
\(
\begin{array}{l|rr}
2 & 6, 8 \\
\hline 2 & 3, 4 \\
\hline 2 & 3, 2 \\
\hline 3 & 3, 1 \\
\hline & 1, 1 \\
\end{array}
\)
\(\Rightarrow LCM = 2 \times 2 \times 2 \times 3 = 24 \) - The LCM of \(6\) and \(8\) is \(24\).
- Convert the fractions to have the same denominator:
\( -\dfrac{5}{6}=-\dfrac{5 \times 4}{6 \times 4}=-\dfrac{20}{24} \)
\( -\dfrac{3}{8}=-\dfrac{3 \times 3}{8 \times 3}=-\dfrac{9}{24} \) - Now compare the numerators.
Since both have negative signs, the smaller numerator is greater.
\(-20<-9\)
Therefore:
\( -\dfrac{20}{24} < -\dfrac{9}{24} \)
Thus:
\( -\dfrac{5}{6} < -\dfrac{3}{8} \)
Ordering of Rational Numbers
Ordering of rational numbers means arranging them from smallest to largest or from largest to smallest.
Same Denominators:
Arrange \(\dfrac{-3}{5}, \dfrac{2}{5}, \dfrac{-1}{5}, \dfrac{4}{5}\) in ascending and descending order.
Solution
\(\dfrac{-3}{5}, \dfrac{2}{5}, \dfrac{-1}{5}, \dfrac{4}{5}\)
First Compare the numerators
\(4>2>-1>-3\)
Now
- Ascending Order: \(\dfrac{-3}{5}, \dfrac{-1}{5}, \dfrac{2}{5}, \dfrac{4}{5}\)
- Descending Order: \(\dfrac{4}{5}, \dfrac{2}{5}, \dfrac{-1}{5}, \dfrac{-3}{5}\)
Different Denominators:
- Find the least common multiple (LCM) of the denominators.
- Convert all fractions to have the LCM as their denominator.
- Compare the numerators and arrange accordingly.
Example:
Arrange \(\dfrac{-1}{3}, \dfrac{2}{5}, \dfrac{-1}{2}, \dfrac{1}{6}\) in ascending and descending order.
Solution
\(\dfrac{-1}{3}, \dfrac{2}{5}, \dfrac{-1}{2}, \dfrac{1}{6}\)
- Since the denominators are different, find the LCM.
\(
\begin{array}{l|rrr}
2 & 3, 5, 2, 6 \\
\hline 3 & 3, 5, 1, 3 \\
\hline 5 & 1, 5, 1, 1 \\
\hline & 1, 1, 1, 1 \\
\end{array}
\) - The LCM of \(3, 5, 2\) and \(6\) is \(30\).
- Now convert the rational numbers to have same denominators.
\( \begin{aligned}
\Rightarrow \dfrac{-1}{3} & =\dfrac{-1 \times 10}{3 \times 10} \\
& =\dfrac{-10}{30}
\end{aligned} \)
\( \begin{aligned}
\Rightarrow \dfrac{2}{5} & =\dfrac{2 \times 6}{5 \times 6} \\
& =\dfrac{12}{30}
\end{aligned} \)
\( \begin{aligned}
\Rightarrow \dfrac{-1}{2} & =\dfrac{-1 \times 15}{2 \times 15} \\
& =\dfrac{-15}{30}
\end{aligned} \)
\( \begin{aligned}
\Rightarrow \dfrac{1}{6} & =\dfrac{1 \times 5}{6 \times 5} \\
& =\dfrac{5}{30}
\end{aligned} \)
- Descending Order: \(\dfrac{2}{5}, \dfrac{1}{6}, \dfrac{-1}{3}, \dfrac{-1}{2}\)
- Ascending Order: \(\dfrac{-1}{2}, \dfrac{-1}{3}, \dfrac{1}{6}, \dfrac{2}{5}\)
FAQs
Yes! Such numbers belong to a category called rational numbers, which can be written as fractions.
Yes! For example, $4$ can be written as $\dfrac{4}{1}$, making it a rational number and an integer at the same time.
Not all decimals are rational numbers. Decimals that terminate or repeat are rational, but decimals that go on forever without repeating belong to irrational numbers.
A rational number is called “rational” because it represents a ratio of two integers (numerator and denominator). It’s all about the fraction!

- Be Respectful
- Stay Relevant
- Stay Positive
- True Feedback
- Encourage Discussion
- Avoid Spamming
- No Fake News
- Don't Copy-Paste
- No Personal Attacks



- Be Respectful
- Stay Relevant
- Stay Positive
- True Feedback
- Encourage Discussion
- Avoid Spamming
- No Fake News
- Don't Copy-Paste
- No Personal Attacks





